Atomic spectra and lasers

In this studio session you will measure the wavelengths of the visible spectral lines in the Balmer series of hydrogen, inspect the spectral lines of helium, neon, and the output of a He-Ne laser, and use a simulation to build a laser.

Equipment needed:

• Demonstration equipment
• Spectral glasses
• Hydrogen discharge lamp
• Ocean Optics Red Tide Spectrometer

Open a Microsoft Word document to keep a log of your procedures, results and discussions.  This log will become your lab report.  Address the points highlighted in blue.  Answer all questions.

Experiment 1

In quantum mechanics confinement leads to energy quantization.  The energy levels of the electron in a hydrogen atom are quantized.  The allowed energies are

E_n = -13.6 eV/n².

When an electron changes from one energy level to another, the energy of the atom must change as well.  This energy can be supplied by a photon whose energy E = hf = hc/λ.

Since the energy levels are quantized, only certain photon wavelengths can be absorbed.  If a photon is absorbed, the electrons will be promoted to higher energy levels and will then fall back down into the lowest energy state (ground state) in a cascade of transitions.  Each time the energy level of the electron changes, a photon will be emitted and the energy (wavelength) of the photon will be characteristic of the energy difference between the initial and final energy levels of the atom in the transition.  The energy of the emitted photon is just the difference between the energy levels of the initial (n_i) and final (n_f) states.
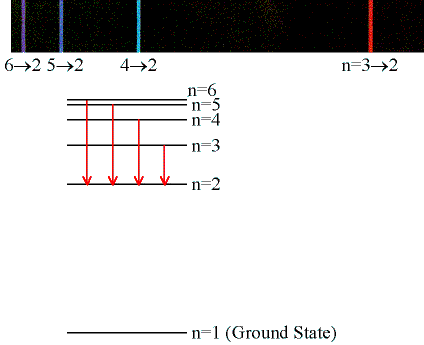
The set of spectral lines for a given final state n_f are generally close together.  The lines for which n_f = 2 are called the Balmer series and many of these spectral lines are visible.  You will be measuring the wavelengths of the Balmer series lines.  The photon energies E = hf for the Balmer series lines are given by the formula

hf = -13.6 eV(1/n_i² - ½²) = 13.6 eV(1/4 - 1/n_i²).

We may write hc/λ = 13.6 eV(1/4 - 1/n_i²), or

1/λ = (13.6 eV/(hc))(1/4 - 1/n_i²) = R(1/4 - 1/n_i²).

The constant R is called the Rydberg constant.  You will determine the Rydberg constant in this experiment.

Plug in and turn on the hydrogen discharge lamp.  Hydrogen gas is excited by a current flowing through the gas.  Look at the light emitted by the excited gas through your spectral glasses.  You will see the line spectrum of hydrogen.

• To measure the wavelengths of the spectral lines, connect the "Red Tide" spectrometer to a USB port of your computer. 
• Open the Spectrometry program.  A shortcut to this program is on the desktop.
• Click "Analyze Light" at the top.
• Bring the fiber close to the lamp.
• Click the record button.  Adjust the position of the fiber until you see a spectrum.
• Click the "Scale to fit" button at the bottom and move the fiber until you see a nice spectrum with several sharp peaks.
  The horizontal wavelength range will be 350 nm to 1000 nm, but only data from ~400 nm to ~ 700 nm are meaningful, since the spectrometer is limited to the visible region.
• When you are satisfied with your spectrum click stop.
• Add a coordinates tool.  Drag it to each peak and record its wavelength.  (The icon for the coordinate tool is at the bottom of the program window.)
  You should see 4 peaks in the visible region with very different intensities.  The peaks correspond to the 4 longest wavelength lines of the Balmer series.  From n_i = 3, 4, 5, and 6 to n_f = 2.  Determine the wavelength of each peak as accurately as possible.
• Note:  First find the wavelength of the two large peaks in the visible region.  Then increase the integration time to see the small peaks in the short wavelength region and find their wavelenths.

Enter each wavelength in units of nm into a spreadsheet.

• Let column D  contain 1/λ.  Let column E contain (1/4 - 1/n_i²).  Into cell E2 type =1/4-1/A2^2 and copy the formula into the other cells of the column.
• Plot 1/λ (y-axis) versus (1/4 - 1/n_i²) (x-axis).  The slope of this graph should be the Rydberg constant R.
• Add a trendline to find the slope.  Display the equation on the chart and set the intercept to be zero.  Format the trendline label, scientific number format, with 3 decimal places.  The slope is your measured Rydberg constant in units of nm^-1.  Paste your plot into your log.
• Calculate the value for R = 13.6 eV/(hc) with hc = 1240 eV nm and compare your measured value with your calculated value.  What is the percent difference?
• Do you understand what you just did?  If not, ask questions.

Note:  If the Spectrometry program is not available, you can use the Capstone program the find the wavelength of the spectral lines hydrogen spectrum by following these instructions.

Exploration 1

Lasers produce highly coherent light via stimulated emission.  A pumping mechanism has to produce a population inversion and a cavity is needed to recycle the photons and increase the probability of stimulated emission.  The class notes introduce you to the He-Ne laser.

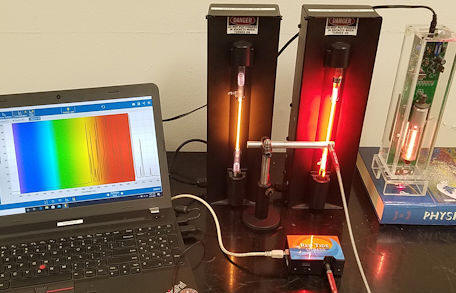
We have use the Red Tide spectrometer to measure 3 line spectra, the spectra emitted He and Ne discharge lamps and the spectrum emitted by a open-cavity He-Ne laser discharge tube.  We have also recorded spectral line of the laser beam.

The spectrum you will analyze was measured using a Red Tide spectrometer.

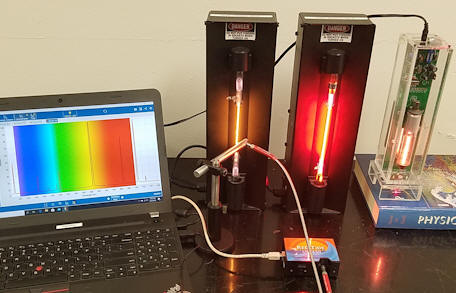Spectrum of He discharge tube	Spectrum of Ne discharge tube
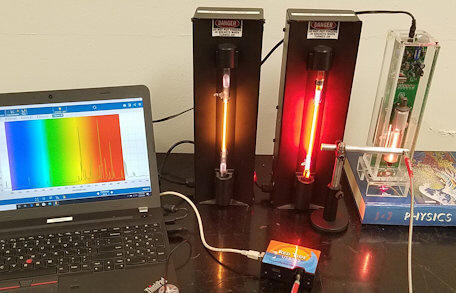Spectrum of He-Ne laser cavity	Spectrum of laser beam shining into the fiber

Download the spreadsheet He-Ne.xlsx and open it.  Examine plots of the spectra.

• Does the He-Ne spectrum contain lines from both He and Ne?
• Do the lines have the same relative strength, or does the strength of some lines depend on the gas mixture?
• Neon is the lasing gas.  Is the laser line a prominent line in the Ne spectrum?

Even a weak line in the spectrum of a gas can become a laser line if the conditions for stimulated emission are met. 

Exploration 2

The class notes introduce you to a 4-level optical pumping scheme.  In a 4-level scheme, the upper laser level may or may not be metastable.

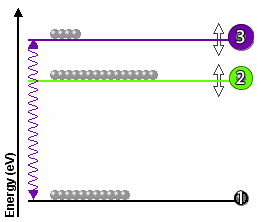3-level optical pumping schemes are also possible, but in a 3-level scheme the upper laser level has to be long-lived or metastable.
In the diagram on the right, a 3-level optical pumping scheme is shown.  Level 3 is the metastable upper laser level.

Use an on-line simulation from the University of Colorado PhET group to build a laser.
Link to the simulation http://phet.colorado.edu/en/simulations/lasers.

• Non obvious control:  You can grab the lines of the excited states in the energy level diagram and move them up and down.

Open the One Atom Panel in the Laser Simulation and start exploring the two-level atom.

• You are optically pumping an atom.  Use the preset wavelength and move the lamp control to a medium level.  Monitor the photons emitted by the atom.  Do you observe spontaneous emissions, stimulated emissions or both?  How can you tell?
• Move the lamp control to a low level.  What do you notice about the emitted photons?
• Move the lamp control to a high level.  What do you notice about the emitted photons?
• Decrease the lifetime of the atom.  What do you notice about emissions?
• Change the wavelength?  What happens?

Explore the three-level atom.

• Turn off the red lamp and try pumping the atom with the blue lamp.  Characterize the emitted photons.
• Click on "display photons emitted from upper state."  Characterize those photons.
• Change the lifetime of the upper state or lower state.  What happens?

Switch to the Multi-Atom Panel and build a laser.

You want to produce many identical photons.  Describe what you have to do to achieve this goal.
First try to establish a population inversion.

• How many energy levels do you need?
• Which energy level do you need to pump?
• Do any of the energy levels have to be metastable?
• Does adjusting the energy level and the wavelength of the pump photons and the emitted photons change the ease with which you can achieve a population inversion?

Now build a laser.

• Do you need mirrors?  Do they need to be highly reflective?
• Can you blow up your laser?  (It takes a long time!)

Convert your log into a lab report.  See the grading scheme for all lab reports.

Name:
E-mail address:

Laboratory 11 Report

• In one or two sentences, state the goal of this lab.
• Make sure you completed the entire lab and answered all parts.  Make sure you show your work and inserted and properly labeled relevant tables and plots.
• Add a reflection at the end of your report in a short essay format.

Save your Word document (your name_lab11.docx), go to Canvas, Assignments, Lab 11, and submit your document.